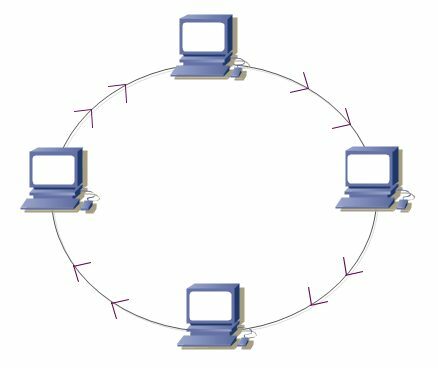
ნებისმიერ კომპიუტერულ ქსელში, თქვენ უნდა გადაწყვიტოთ ტოპოლოგია. ქსელის ტოპოლოგია არის ფიზიკური არქიტექტურა, თუ როგორ უკავშირდებიან კომპიუტერები ერთმანეთს. კლასიკური ქსელის ტოპოლოგია არის რგოლის ტოპოლოგია. ამ სტრუქტურაში, ქსელის ყველა მოწყობილობა დაკავშირებულია ერთ რგოლში. მთელი ქსელის ტრაფიკი მიდის ერთი მიმართულებით მარყუჟის გარშემო. ეს ნიშნავს, რომ თითოეულ მოწყობილობას აქვს ორი კავშირი ქსელთან, ერთი, რომელიც იღებს მონაცემებს და მეორე, რომელიც გადასცემს მონაცემებს.
სარგებელი
რგოლის ტოპოლოგია შედარებით მარტივი დასაყენებელია, ყოველ შემთხვევაში მცირე მასშტაბებზე. მაგალითად, თუ ფიქრობთ ოფისში თითოეული კომპიუტერის გვერდით მდებარე კომპიუტერთან დაკავშირებაზე, ამის გაკეთება შედარებით მარტივი იქნება. კონცეფციის განხორციელება კიდევ უფრო ადვილი ხდება rack სერვერებით. სირთულე ჩნდება სხვადასხვა ოთახებში, სართულებსა თუ შენობებში ქსელებთან ურთიერთობისას, სადაც შეიძლება უფრო რთული იყოს კაბელების გაშვება.
რგოლების ტოპოლოგიის ქსელებში არ არის საჭირო შეჯახების აღმოჩენის ან შეჯახების თავიდან აცილების ტექნოლოგიები, როგორც თითოეულმა მოწყობილობამ უკვე იცის გადასცემს თუ არა მონაცემებს და, შესაბამისად, შეუძლია თუ არა მეტის გადაცემა. არ არის საჭირო ცენტრალური სერვერი ან როუტერი მოწყობილობებს შორის კავშირის სამართავად.
ნაკლოვანებები
იმის გამო, რომ ქსელის ტრაფიკი მიედინება მხოლოდ ერთი მიმართულებით, მთელი ტრაფიკი ერთხელ უნდა გაიაროს მარყუჟის გარშემო. მიუხედავად იმისა, რომ განზრახ მიმღებს შეეძლო დაედგინა შეტყობინება, როგორც მისთვის განკუთვნილი და არ გადასცეს ის, თუ ასე მოიქცეოდა, გამგზავნს არ ექნება საშუალება გადაამოწმონ, რომ შეტყობინება მიღებული იყო თუ არა. ეს ხარჯავს სიჩქარეს, რამაც შეიძლება გამოიწვიოს პრობლემები მძიმედ დატვირთულ ქსელებში.
მოწყობილობის ნებისმიერ უკმარისობას შეუძლია მთელი მარყუჟის დაშლა. თუ ყველა შეტყობინებას სრული მარყუჟის დასრულება სჭირდება, თუ ციკლში სადმე შეფერხებაა, ყველა შეტყობინება წარუმატებლად გამოჩნდება. ტექნიკურად, ზოგიერთმა შეტყობინებამ შესაძლოა მიაღწიოს მის მიმღებს, თუ ისინი ადრე იყო ციკლში, ვიდრე წარუმატებლობა, თუმცა, გამგზავნს არ აქვს ამის გაგების საშუალება. ეს საკითხი ძირითადად შეიძლება მოგვარდეს ორმხრივი მარყუჟის ან კონტრ-ბრუნი რგოლის ტოპოლოგიის ვარიანტით, რომელიც განხილულია ქვემოთ.
რგოლზე რაიმე სახის კორექტირება იწვევს შეფერხებას, დროებით არღვევს მთელ რგოლს. ვინაიდან თითოეულ მოწყობილობას აქვს მხოლოდ ორი კავშირი, ახალი მოწყობილობის დამატება ან ძველის ამოღება, იწვევს ქსელის შეფერხებას, მთელი რგოლის გათიშვას, სანამ კავშირი არ აღდგება.
სამწუხაროდ, ეს ასევე ნიშნავს, რომ ყველა მოწყობილობა უნდა დარჩეს ჩართული. თუ კომპიუტერი გამორთულია, მისი ქსელის ბარათი აღარ გადასცემს შეტყობინებებს. ეს არღვევს რგოლს, რაც რგოლების ტოპოლოგიას შეუფერებელს გახდის ქსელებისთვის, რომლებსაც არ აქვთ თითქმის სრულყოფილი დრო. მთლიანი რგოლი მარცხის დროს, როდესაც ერთი ბმული ვერ ხერხდება, ასევე ხდის მათ შეუფერებელს დისტანციური მართვისთვის, რადგან ნებისმიერი დისტანციური წვდომა, როგორც წესი, ეყრდნობა გატეხილ მარყუჟს.
კომუნიკაციის შეყოვნება პირდაპირპროპორციულია მარყუჟში არსებული მოწყობილობების რაოდენობისა. თითოეული ჰოპი, რომელიც ქსელის პაკეტს სჭირდება, ზრდის დანიშნულების ადგილზე მისასვლელად საჭირო დროს.
ვარიანტები
ორმხრივი მარყუჟი ან საპირისპირო მბრუნავი რგოლის ტოპოლოგია არის რგოლის ტოპოლოგიის ვარიანტი, რომელსაც აქვს მეორადი მარყუჟი, რომელიც გადასცემს ქსელის ტრაფიკს მარყუჟის გარშემო პირიქით. როგორც წესი, ეს მეორადი მარყუჟი არ გამოიყენება, თუ მთავარი მარყუჟი არ არის გატეხილი. შესვენების აღმოჩენის შემდეგ, შესვენებასთან უახლოესი სამუშაო მოწყობილობა მარშრუტებს ნებისმიერ მოძრაობას მარყუჟის გარშემო, არსებითად ქმნის "C" ფორმის მარყუჟს.
თეორიულად, მეორადი მარყუჟი ასევე შეიძლება გამოყენებულ იქნას დამატებითი გამტარუნარიანობის უზრუნველსაყოფად, თუმცა ეს ზოგადად არ კეთდება. მიუხედავად იმისა, რომ მეორე მარყუჟის უზრუნველყოფა შესაძლებელია თითოეულ მოწყობილობასთან მავთულის სხვა წყვილის შეერთებით, ეს ასევე, როგორც წესი, არ კეთდება, რადგან ეს აორმაგებს რგოლისთვის საჭირო ინფრასტრუქტურას. ამის ნაცვლად, ორმხრივი კომუნიკაცია ერთ კაბელზე ჩართულია სრული დუპლექსური კომუნიკაციის გამოყენებით. ეს ხელს უწყობს შეცდომების ტოლერანტობის უზრუნველყოფას მარყუჟში, მაგრამ არ ეხება მასშტაბის სირთულეებს ან შეყოვნების საკითხს.
სიმბოლური რგოლის ტოპოლოგია შეიძლება ადვილად ავურიოთ ბეჭდის ტოპოლოგიასთან, თუმცა, ისინი ძალიან განსხვავდებიან. სახელის მიუხედავად, სიმბოლური რგოლის ქსელი რეალურად იყენებს ვარსკვლავურ ტოპოლოგიას ფიზიკური კავშირის ფენაში.
დასკვნა
ბეჭდის ტოპოლოგია არის კომპიუტერული ქსელის არქიტექტურა, რომელიც ათავსებს ყველა მოწყობილობას ერთ რგოლში. მთელი ქსელის ტრაფიკი ერთი მიმართულებით გადაიცემა რგოლის გარშემო, რაც აადვილებს მცირე, ლოკალური ქსელების დაყენებას. თუმცა, ტოპოლოგია იბრძვის მასშტაბით და ქსელში არსებული თითოეული მოწყობილობა არსებითად მოქმედებს როგორც ერთი მარცხის წერტილი, რომელსაც შეუძლია მთელი ქსელის დაშლა. ამ მიზეზების გამო, რგოლის ტოპოლოგიები ახლა ძალიან იშვიათად გამოიყენება, თუ საერთოდ. ვარსკვლავური ტოპოლოგიის ქსელები, როგორც წესი, გამოიყენება ბოლო წერტილებისთვის, ხოლო უკანა ქსელები იყენებენ ქსელურ ტოპოლოგიას.